Now they say it is shaped like a trumpet

At first they thought it was flat. Then that it was shaped like a football. But now, scientists believe the universe could be shaped like a flat-sided trumpet.
 |
That would lead to strange effects in some parts of the universe, where time and light would be so curved that you could see the back of your own head. Also, a long-held theory about the universe - that it looks much the same anywhere - would have to be abandoned. And finally, the universe would be finite, rather than extending in every direction forever.
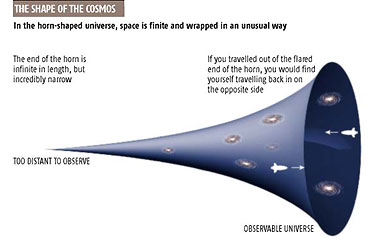
The new shape, predicted by careful mathematical modeling to fit with known astronomical data, would have the universe stretched out into a long funnel, flaring into a bell-like shape at one end. The thin end would be infinitely long - but so narrow that it would have a finite volume.
The "bell" of the trumpet would also be peculiar: it would flare out, but a spaceship that could somehow navigate towards the open end would eventually find itself flying back along the "outside surface" of the bell.
The research by a team of German physicists led by Frank Steiner at the University of Ulm is reported in New Scientist magazine.
Their theory uses a complex mathematical model called a "Picard topology", named after a mathematician rather than the Star Trek character. It would mean the universe has a finite volume, although you would not be aware of its "edges"; they would seem to be part of the rest of space.
The concept follows a close examination of the dramatic data produced by Nasa, the US space agency, in 1996, which showed that the very faint microwave radiation left over from the Big Bang 13 billion years ago was not evenly spread throughout the cosmos. This lack of evenness - called "anisotropy" - suggested that large-scale models of the shape of the universe, previously thought to be a flat expanse of space-time, were wrong.
Ever since then, cosmologists have puzzled over what the data from the Cosmic Background Explorer (Cobe) spacecraft could tell them about the space-time "shape" of the universe. One rival group proposed last year that the universe was shaped instead like a football. But that would have left a particular pattern of background radiation - which has not been found by further experiments.
In the "flat" space of conventional cosmology, small "blobs" - hot and cold spots - in background radiation should be round. But observations show that instead they are ellipses. The curve of a horn-shaped universe can explain this, says Professor Steiner.
The "space" in any small part of the "horn" is saddle-shaped, like a Pringles potato crisp. Such a "negatively curved" space would act as a warped lens, distorting the image around the blobs so they look elliptical to astronomers.
Another property of a "trumpet" universe would be that large blobs more than about 60 degrees across would be absent. So far, scientists have also found this to be the case.
But if the team at Ulm is right, scientists will have to abandon one of the fundamental tenets of cosmology - that all parts of the cosmos are about the same. Holger Then, a member of Professor Steiner's team, told New Scientist: "If one happens to find oneself a long way up the narrow end of the horn, things indeed look very strange, with two very small dimensions."
At an extreme enough point, you would be able to see the back of your own head. Over the next year or so, astronomers will test whether large blobs really are lacking in cosmic microwave background radiation and small ones really are elliptical.
Source: The Independent
Additional References:
Big Bang glow hints at funnel-shaped Universe
Additional IslamiCity Notes:
When we see scientific discoveries through the prism of the Quran it helps us in understanding the complexity and awe-inspiring nature of creation. Scientific discoveries are evolutionary, at the same time our belief is that God has sent down the Quran for all ages. As we acquire new knowledge our understanding of creation and how we see them in light of the Quran will transform.
It is interesting to note the following Quranic verses in light of the above discovery about the cosmos.
It is He (God) who created the heavens and the earth in true (proportions): the day He said, "Be," behold! it is. His word is the truth. His will be the dominion the day the trumpet will be blown. He knows the unseen as well as that which is open. For He is the Wise, well acquainted (with all things)
Quran 6:73
The trumpet will (just) be sounded, when all that are in the heavens and on earth will swoon, except such as it will please Allah (to exempt)...
Quran: 39:68
Visit IslamiCity Islam & Science Center
Related Suggestions
is the one that'll be blown by the arch angel Israafeel (aka Raphael).Raphael's trumpet is unrelated to the present trumpet-like shape of the cosmos deduced by Frank Steiner et. al.
Here trumpet means what - what we actually heard is that trumpet referred to the instrument which will be blown by the angel Israfil. could you please explain in detail, it i am wrong.
Jazak Allah Khairan Kaseera
I read the artical, was fine, Some words I did not understand. I dont want to say I am agreed bcos if it is not we cant say ok then that is not the case. Other thin I want tell u is very recently I received email about a sun rises from west on Mars. So just thought to forwatd it if u guys can find the truth about the source of the news
The Emaail is:
Please read, very interesting article.
The science of astronomy states that the speed of planet Mars has been decreasing in its course toward the eastern direction in the few past weeks to the level we notice the "waver" between the east and the west..and on Wednesday the 30th of July the planet movement stopped going toward the eastern direction..
Then in the months of August and September...Mars changed its course in the opposite direction to the West- and that until the end of September..which means the sun will rise now from the west on Mars!!
And this weird phenomena of the opposite movement called "Retrograde Motion" Most scientist state that all the planets will go through the same once at least and our planet Earth is one of them. Planet Earth will move in the opposite direction some day and the sun will rise from the west!!
This might occur soon and we are unaware!
The rise of the sun from the west is mentioned in the hadith and this is the major sign of the day of judgment, most if not All, the minor signs have occured. Wake up.
Our beloved messenger Mohamed (Peace Be Upon Him) said: "One of the signs of the hour..the sun will rise from the west, where no longer tauba (forgiveness) will be granted" !!
And the strange thing..most of our Shariah scholars mentioned that the rise of the sun from the west occurs only once..on that day..the sun will rise from the west..then again from the east..and continues until Allah wishes..and this is similar to what is happening to Mars..it stops, then it changes its course of direction for a short
We live in one fo the most exciting ages in human history,according to my understanding.
All else has been purposed with intense intent of understanding except our Universe and the Bestower of the Realm. What else is there to engage in except the enormity of our ignorance and the directives, by the Grace of God, to transcend mundane interests and attempt to approach the exactness of a worthy life's pursuit.
On day someone might discover that at the end of the narrow side of the trumpet, there starts infinity.
Man must know his minds,which is ever changing.
I think that comment you made was uncalled for and it really only makes you seem uneducated or brutish. How might that comment make an innocent American feel (such as one who is a fellow believer)? I would have been much more interested to hear a constructive criticism of the subject at hand than to read your rantings.
By the way, the article is interesting and I am reading all of the comments.
What a news for the Zionists and the American thugs!!!
It is good to see that you try to show that everything is in the Quran,existing(eventhough you do not need it).However as Ahmed said do not apply
that every single detail.You know that this is just a theory it can be proven or disproven.Therefore if you compare it with Quranic verses you might actually can show something does not exist as it is existing and misguide the people.Ofcourse Allah(C.C) knows the best and He just revealed the truth yet the Quran is not an easy book that we can fully understand and even scientists can.As you know in science every discovery corrupts the old one so we can not jump to the conculusion.Today science tries to answer some paradoxes that it has put forward such as the root of humanity.First human sample has changed many times and expected to change so it is not good to rely on science while Quran lies there for us. Jazakumullah Khair, we all know you have good intentions.First of all it is the intention that counts however just we need to be bit more patient before we try to do something for Islam.Especially the media groups should be very careful and picky about their articles.
Vassalam
Its a interesting article,but we should becarefull with the new scientific theory. Scientific theory will always growth, a new theory would be a old theory and nobody use it again. but thats a gr8 service, thanks
Wassalamu'alikum
We should be careful and not compare the Holy Scriptures to scientific discoveries. Science can contradict itself and/or reposition it's theories as new information becomes apparent, "today's cosmology is tomorrow joke".
Allah SWT knows best,
Ahmad:
My understanding is, if we want to be very precise, then Calculus has its limitations! And mathematicians are well aware of it!! One of my math prof once said, " We all do cheating and mathematicians are no exceptions" !!
Well this was explained but its still interesting how the universe who form a trumphant and the end would be infinitely narrow. Hmm how interesting....
The Big Bang is now a scientific fact and not mere theory anymore. This is a fact that will not change, just like the Earth being round.
Allah SWT mentioned it to us more than 1400 years
ago in the Glorious Quran. For more details check out Dr. Zakir Naik's lectures.
SubhanAllah!! Can we extend this theory with the What Allah Subhana Ta'ala says in Qur'an that the trumpet will be blown in Dooms day!! All glory belongs only to Allah, The Almighty.
We must be wary about reading too much into what people of science promote.
Having spent a life long passion of understanding Physics and Allah's Law, I have realised that 'no scientist was ever wrong!'
How can this be?
Well the answer lies in the Quran, in which Allah, plainly tells us, that He is the Master of All Perceptions.
This means that no matter how we want to explain our existence, the universe etc.
Allah will make our perception become valid and show the limitless nature.
A bit like living in a kaleidoscope.
So every theory to explain the universe is true, for us, because Allah makes it so.
The real reality is not our universe, at all.
"And the trumpet is blown", could well be the universe being flushed out.
But why is it blown?
That is what we, as muslims, can answer.
The reality is the 'deeds' we committed when we were alive, on Earth, not the Earth which nurtured us.
It was a mere Perception of the Almighty, the Tremendous.
Dear brothers and sisters
When the Big bang theory was dominant, many clerics found proves in AL-Quran for it. Is it that AL-QURAN is wrong. Lets remember that sciense is ever changing, and we should be carefull with combining theories with the holy measage. Sciense is oppening doors to wonders of ALLAH swt. and we should all appriciate that.
ALLAH HAFIZ
p.s. this does nothing to prove the existence or non-existence of god!
LA HAWLA WALA QUWATA ILLAH BILLAH!!!!!!!!!
Assalamu alaikum
Ya! thats true, as told by a famous us scientist
"THERE MUST BE ONE POWER, THAT POWER NOT INSIDE THE UNIVERSE OR THE UNIVERSE NOT CONTAINING THAT CREATER, HE IS BEYOND THE UNIVERSE...BCOS EACH AND EVERY CORNER OF THE WHOLE UNIVERSE THERE IS A PERFECT ORDER WHICH CAME INTO EXISTANCE BY MERE CHANCE, BCOS THE UNIVERSE IS EXPANDING IN CRITICAL LEVE." SUUHANALLA.
o ALLAH WE DONT KNOW WHAT YOU HAVE THOUGHT US.YOU ARE ALL-KNOWING AND ALL-WISE AL-QURAN(SURA BAKHRA)
Lets assume there is no God.
This implies that nothing in the universe has been created.
If this is so, then the universe and everything within it has existed since eternity.
However, in the twentieth century, this notion of the eternal existence of our universe has been proven completely wrong by the 'Big Bang Theory'. It is now a well-established fact of Physics based on rigorous mathematical arguments and astronomical observations that the universe that we see has a definite beginning. So, the universe had a beginning. A solid contradiction!
We can also have a direct contradiction if we assume that the universe existed for eternity. Let's assume it!! Then, if 't' is the age of the universe (with all its contents we consider them a single set), then it must be that the limit of 't' approaches infinity. If the age of the universe approaches infinity, than all its contents must also exist since infinity. But you will immediately say that no plants or animals exist for infinity. They have a definite beginning and an ending within their domain of the universe. Lo and behold!!! We have a contradiction! Hence the universe cannot exist for infinity.
Therefore, the universe has a beginning (as decisively proven by both Big Bang Theory or simple logical arguments). If the universe has a beginning, then we have two options:
1) It spontaneously generated.
2) It has been created.
The first option implies self-creation out of nothing. If it has been the case, then the universe known to us would immediately collapse. If a 'Big Bang' can spontaneously occur once, why isn't it happening again!! Thus the primary elements around us show any sign of self-generation, let alone coming out of nothing? The answer is
Peace!